What is the Central Limit Theorem and what is the formula to calculate the Central Limit Theorem?

Table of Contents

Introduction:

Are you trying to understand statistics better? One concept that is essential to master is the Central Limit Theorem. But what is the Central Limit Theorem, and what is the formula to calculate it? Don’t worry, we’ve got you covered. In this article, we will explore this fundamental statistical concept and the formula used to calculate it. You’ll learn how this theorem plays a critical role in understanding data distribution and probability. So, let’s dive in!

What is the Central Limit Theorem?

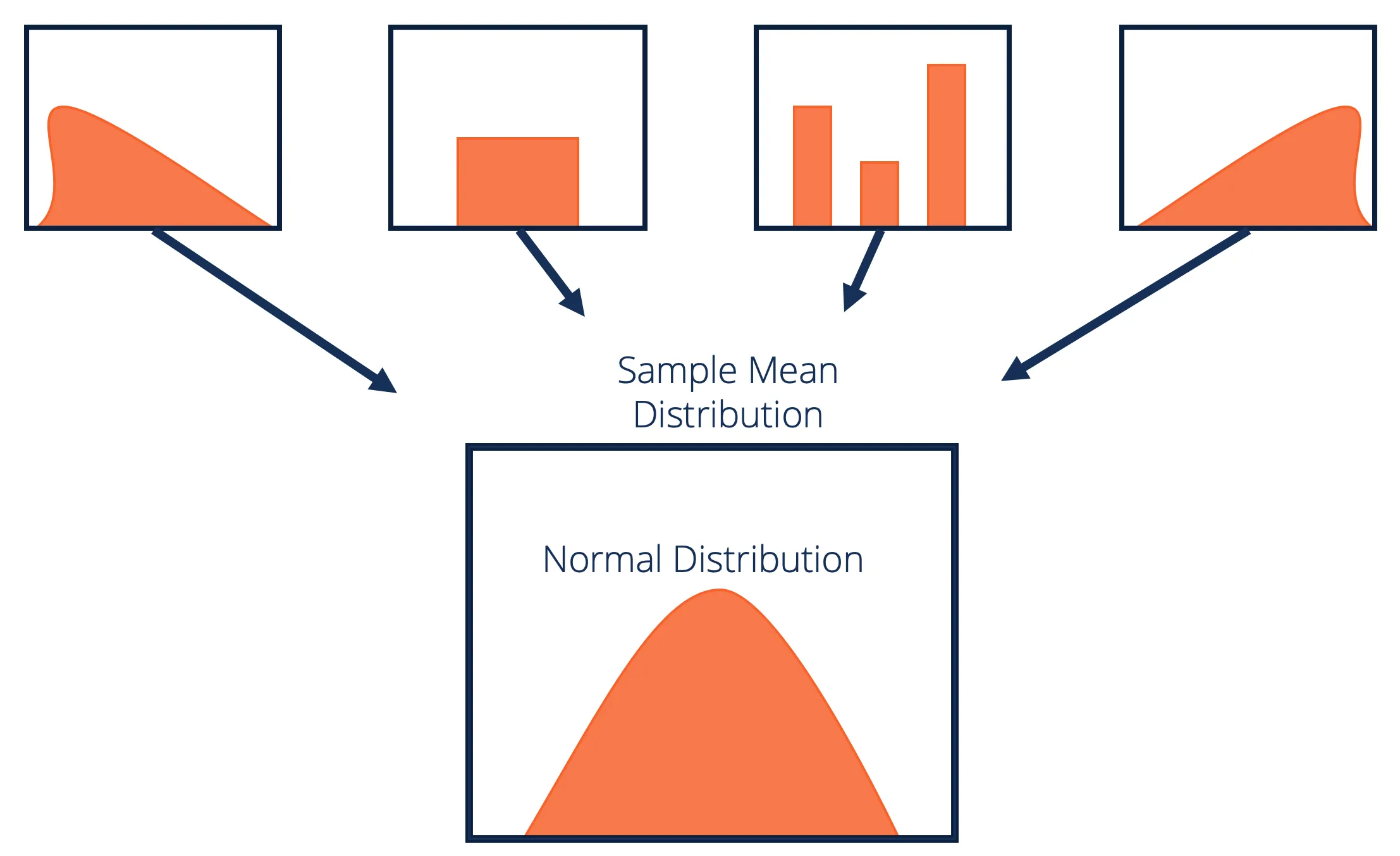
The Central Limit Theorem (CLT) is a fundamental concept in statistics that describes the behavior of the mean of a large sample of independent, identically distributed random variables. In other words, it helps us understand how the means of samples behave when taken from a larger population.

The CLT states that the distribution of sample means approximates a normal distribution as the sample size increases, regardless of the population’s underlying distribution. This means that, given a large enough sample size, the sample means will cluster around the population mean and follow a bell-shaped curve.

The Central Limit Theorem plays a critical role in statistical analysis and is used extensively in hypothesis testing, confidence intervals, and other statistical calculations.

What is the formula to calculate the Central Limit Theorem?

The formula to calculate the Central Limit Theorem is relatively straightforward. Suppose you have a population with a mean (μ) and a standard deviation (σ). In that case, the mean of a sample of size n taken from that population (x̄) can be calculated using the following formula:

x̄ = (x1 + x2 + … + xn) / n

Where x1, x2, …, xn are the values of the n observations in the sample.

To calculate the standard error (SE) of the sample mean, we use the following formula:

SE = σ / sqrt(n)

Where σ is the population standard deviation and sqrt(n) is the square root of the sample size.

Finally, we use the following formula to calculate the z-score, which is the number of standard deviations that the sample mean is from the population mean:

z = (x̄ - μ) / (SE)

The z-score allows us to calculate the probability of observing a sample mean as extreme as the one we have calculated, assuming the null hypothesis is true.

Bullet Points:

The Central Limit Theorem helps us understand how the means of samples behave when taken from a larger population.
The distribution of sample means approximates a normal distribution as the sample size increases, regardless of the population’s underlying distribution.
The Central Limit Theorem is used extensively in hypothesis testing, confidence intervals, and other statistical calculations.
The formula to calculate the Central Limit Theorem involves calculating the mean of a sample, the standard error, and the z-score.

FAQs:

Q: Why is the Central Limit Theorem important?

A: The Central Limit Theorem is important because it allows us to make inferences about a population based on a sample. It is used extensively in hypothesis testing, confidence intervals, and other statistical calculations.

Q: Can the Central Limit Theorem be applied to any population distribution?

A: Yes, the Central Limit Theorem can be applied to any population distribution, regardless of its shape or type.

Q: How does sample size affect the Central Limit Theorem?

A: As the sample size increases, the distribution of sample means becomes more and more normal, which means that the Central Limit Theorem becomes more and more accurate. In other words, larger sample sizes lead to more reliable estimates of population parameters.

Q: What is the significance of the z-score in the Central Limit Theorem?

A: The z-score is significant in the Central Limit Theorem because it allows us to determine how likely it is that a sample mean is due to chance or random variation. By calculating the z-score, we can calculate the probability of observing a sample mean as extreme as the one we have calculated, assuming the null hypothesis is true.

Conclusion:

In conclusion, the Central Limit Theorem is a fundamental concept in statistics that describes the behavior of the mean of a large sample of independent, identically distributed random variables. It helps us understand how the means of samples behave when taken from a larger population and plays a critical role in statistical analysis. The formula to calculate the Central Limit Theorem involves calculating the mean of a sample, the standard error, and the z-score. By understanding and applying the Central Limit Theorem, we can make more accurate inferences about a population based on a sample.